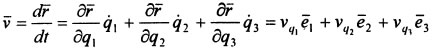6) Определение скорости точки при задании в криволинейных координатах. Пример.

Скорость точки М при задании ее движения в криволинейных координатах определится в виде векторной суммы составляющих скоростей, параллельных координатным осям: 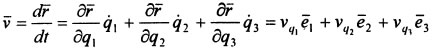. Проекции скорости на соответствующие координатные оси равны: . Модуль скорости в ортогональной криволинейной системе координат можно рассчитать по зависимости: . В приведенных формулах значения производных и коэффициентов Ламе вычисляют для текущего положения точки М в пространстве.

Пример (может быть и не это): Скорость в сферической системе координат.

Координатами точки в сферической системе координат являются скалярные параметры r, "фи", "тета", отсчитываемые так, как показано на рис. Система уравнений движения точки в данном случае имеет вид: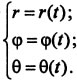

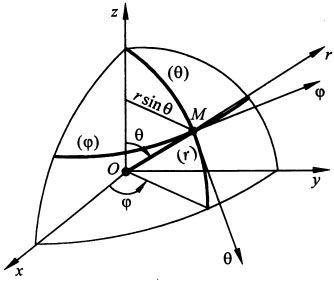
На рис. изображены радиус-вектор r, проведенный из начала координат, углы "фи" и "тета", а также координатные линии и оси рассматриваемой системы в произвольной точке М траектории. Видно, что координатные линии ("фи") и ("тета") лежат на поверхности сферы радиусом r. Данная криволинейная система координат также является ортогональной. Ее оси Mr, М("фи") и М("тета") и соответствующие им единичные векторы er, e("фи"), е("тета"), определяютщие положительные напревления осей, взаимно перпендикулярны. Декартовы координаты могут быть выражены через криволинейные координаты так: . Тогда коэффициент Ламе: ; проекции скорости точки на оси сферической системы координат , а модуль .

Дополнение:

Движение точки в пространстве можно считать заданным, если известны законы изменнеия трех ее декартовых координат x, y, z как функции времени. Однако в некоторых случаях пространственного движения материальных точек (например, в областях, ограниченных поверхностями различной формы) использование уравнений движения в декартовых координатах неудобно, так как они становятся слишком громоздкими. В таких случаях можно выбрать другие три независимых скалярных параметра q1, q2, q3, называемых криволинейными, или обобщенными координатами, которые также однозначно определяют положение точки в пространстве.

Положительные направления координатных осей задаются единичными векторами, которые называются базисами. Они определяются через частные производные от радиус-вектора точки по i-ой обобщенной координате в данной точке M: 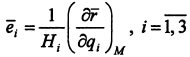. Здесь 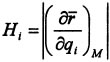- параметр, который называется i-ым коэффициентом Ламе и равен значению модуля частной производной от радиус-вектора точки по i-ой криволинейной координате, вычисленной в данной точке М. Каждый из векторов ei имеет направление, соответствующее направлению движения точки конца радиус-вектора riM при возрастанийй i-ой обобщенной координаты.

(подробнее про криволиненые координаты)

Проекции ускорения точки М на оси криволинейной системы координат определяют по формуле: 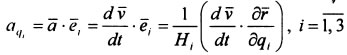. Ускорение точки при задании ее движения в криволинейных координатах определится в виде векторной суммы составляющих ускорений, параллельных осям этой системы координат, , где aqi - проекции ускорения на оси, определяемые по формуле: 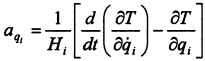, i=1,3. Модуль ускорения в ортогональной криволинейной системе координат вычисляется по формуле: .

Проекции ускорения на оси сферической системы координат 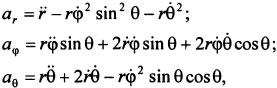,а модуль .