26) Сложное вращение твердого тела вокруг параллельных осей.

Если оси вращательных движений тела параллельны, то вектор результирующей угловой скорости тела в неподвижной системе координат, определяемый согласно , будет колпинеарен векторам ее составляющих и . Положение мгновенной оси вращения тела как оси, проходящей через неподвижную в данный момент точку Р тела, т. е. точку его МЦС в плоскости П, перпендикулярной осям вращений (рис. 7.3), можно определить из следующего анализа.

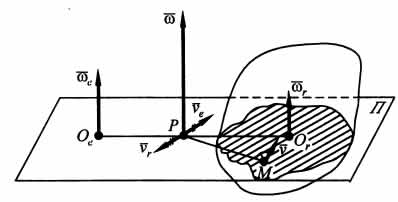
Относительная скорость точки Р , а переносная . Здесь Оr и Ое — точки пересечения плоскости П с соответствующими осями вращения. Тогда скорость точки Р в неподвижной системе координат , причем, согласно определению МЦС, vP = 0 . Отсюда следует . В зависимости от взаимного расположения и численного значения векторов и можно выделить три случая сложения вращательных движений.

1) При совпадении направлений векторов и абсолютное движение будет плоским.

Абсолютная угловая скорость в этом случае будет иметь направление, совпадающее с направлениями ее составляющих, а ее модуль . Точка Р, через которую проходит мгновенная ось вращения тела, лежит на отрезке, соединяющем точки Оr и Ое. При этом и положение точки Р можно найти из пропорции: . Скорость любой точки тела, например M, в данном случае может быть найдена по формуле , а ее модуль — кратчайшее расстояние от точки до мгновенной оси вращения, проходящей через точку Р.

2) При противоположных направлениях векторов и , когда не равно, абсолютное движение, как и в первом случае, будет плоским.

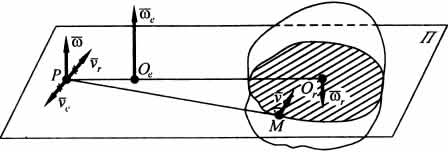
Абсолютная угловая скорость при этом будет иметь направление, совпадающее с направлением большей по модулю составляющей угловой скорости, а ее модуль .
Точка P, через которую проходит мгновенная ось вращения тела, лежит в плоскости П, перпендикулярной осям вращательных движений, на прямой, проходящей через точки Ое и Ог; расположена она внешним образом по отношению к этим точкам со стороны той точки, через которую проходит ось вращения движения с большей угловой скоростью. При этом . Пропорции для нахождения положения точки Р имеют вид

3) При противоположных направлениях векторов омега переносное и омега радиальное и равенство их модулей, если условие выполняется на отрезке времени t2-t1, абсолютное движение будет поступательным. Такой случай сложения вращательных движений называется парой вращений.

.