Принцип возможных перемещений.
Аналитические условия равновесия механических систем были сформулированы Ж. Лагранжем в его фундаментальной работе «Аналитическая механика» (1788 г.) как «принцип возможных скоростей». В настоящее время принцип, определяющий в общей форме условия равновесия системы, называется принципом возможных перемещений, или принципом Лагранжа: чтобы данное положение механической системы со стационарными идеальными связями было положением равновесия, необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении системы из этого положения была равна нулю.
Однако принцип возможных перемещений позволяет находить и реакции идеальных связей. Для этого, в соответствии с принципом освобождаемости, связь отбрасывают, заменяя ее соответствующей реакцией. Эту реакцию включают в число активных сил. При отбрасывании связи увеличивается число степеней свободы системы. Поэтому точке приложения реакции отброшенной связи можно задать возможное перемещение. К системам с неидеальными связями принцип возможных перемещений неприменим. Однако в некоторых случаях, например при движении точки по шероховатой поверхности, связь рассматривают как идеальную, дополняя ее силой трения скольжения.
Из лекций:
Принцип возможных перемещений (Лагранжа): Для равновесной механической системы. подчиненной голономным связям (геометрические, интегрируемые кинематические = голономные), идеальным (если у какой-то связи 
(RK тоже вектор), то связь называется идеальной), стационарным (связь называется стационарной или склерономной, если время t не входит явно в уравнение связи) и неосвобождающим (жестким) связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил приложенных к точкам системы была равна еулю на любом возможном перемещении системы.
Доказательство необходимости:
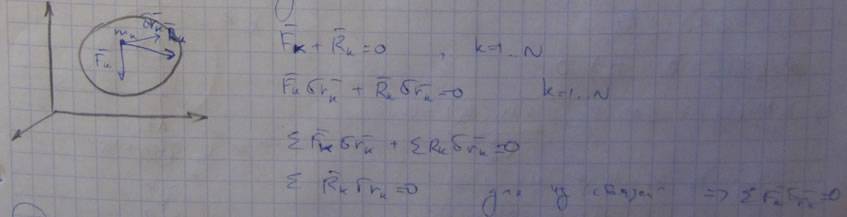
Доказательство достаточности:
Предполагаем, что одна из точек находится не в равновесии.
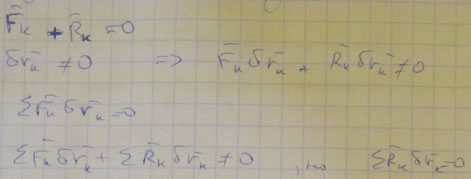, что противоречит условию.