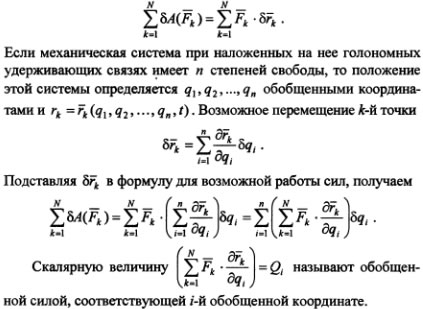
Обобщенные силы. Способы вычисления обобщенных сил.

В аналитической механике наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело со стороны других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим возможную работу сил, приложенных к точкам системы,

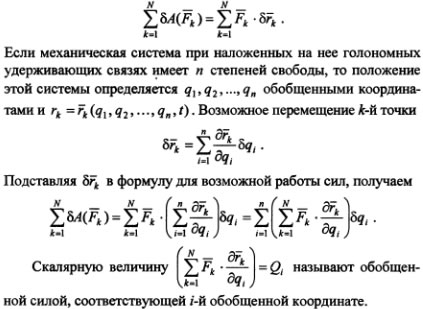
Таким образом, обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему.

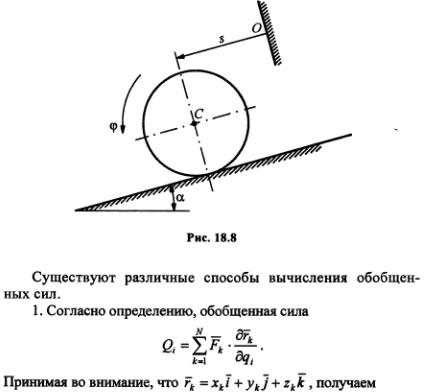
В общем случае обобщенная сила является функцией обобщенных координат, скоростей точек системы и времени. Из определения следует, что обобщенная сила — скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Так, для диска радиусом r и массой m, который катится без скольжения по наклонной плоскости (рис. 18.8), за обобщенные координаты можно принять либо s — координата центра масс диска, либо "фи" — угол поворота диска. Если пренебречь сопротивлением качению, то в пер-

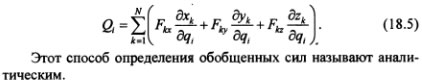
2. Обобщенные силы для механических систем с n > 1 целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации независимы между собой. Системе всегда можно сообщить такое возможное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае:

Из лекций:

Из интернета:

Суммируя виртуальные работы по всем обобщенным координатам, найдем виртуальную работу сил системы в обобщенных координатах:

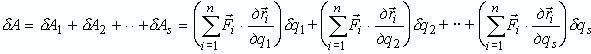(3)

Обозначая коэффициенты при приращениях или вариациях обобщенных координат как Q1, Q2, ..., Qs, выражаем виртуальную работу сил системы в обобщенных координатах в виде

(4)

Обобщенные силы и способы их вычисления. В аналитической механике обобщенными силами называются коэффициенты Q1, Q2, ..., Qs при приращениях или вариациях обобщенных координат в выражении (4) виртуальной работы сил системы в обобщенных координатах.

Обобщенная сила Qj в общем случае не является силой в обычном понимании. Ее размерность зависит от размерности обобщенной координаты qj и определяется равенством [Qj] = [A] / [qj], где [A] - размерность работы. Так, если обобщенная координата - линейная величина, то обобщенная сила имеет размерность силы. Если обобщенная координата - угловая величина, то обобщенная сила имеет размерность момента, а если обобщенная координата является, например, объемом камеры сгорания над поршнем двигателя, то обобщенная сила имеет размерность давления.

Рассмотрим основные способы вычисления обобщенных сил.

Первый способ аналогичен тому, что мы применяли для вычисления виртуальной работы сил системы в обобщенных координатах. Системе дается виртуальное перемещение так, чтобы изменялась только первая обобщенная координата при фиксированных остальных обобщенных координатах. На этом виртуальном перемещении подсчитывается виртуальная работа сил системы. Коэффициент при вариации первой обобщенной координаты в выражении этой работы будет обобщенной силой по первой обобщенной координате. Аналогично поступают и для остальных обобщенных координат, определяя каждый раз коэффициенты при вариациях обобщенных координат в выражениях виртуальной работы, которые будут представлять собой обобщенные силы по соответствующей обобщенной координате.

Второй способ используется для голономных систем со стационарными связями, когда обобщенные скорости могут совпадать с виртуальными обобщенными скоростями, то есть

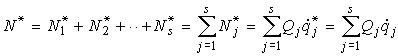(7)

Из (7) видим, что обобщенными силами будут коэффициенты при обобщенных скоростях в выражениях виртуальной мощности сил системы по каждой обобщенной координате, вычисляемой при не равной нулю обобщенной скорости по данной обобщенной координате (qj' <> 0), когда остальные обобщенные скорости равны нулю (qk' = 0 (k <> j)).

Третий способ основан на выражении обобщенных сил в координатной форме. Записав (3) в виде

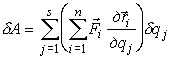(8)

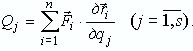(9)

Выразив (9) в аналитической форме записи, получаем формулу для вычисления обобщенных сил в координатной форме:

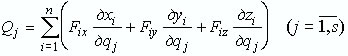(10)

Четвертый способ применяется тогда, когда большинство сил системы потенциальны. В этом случае потенциальная энергия системы является функцией обобщенных координат, то есть П = П(q1, q2, ..., qs), а

(11)

Примечание: при вычислении обобщенных сил первым или вторым способами приращения (вариации) обобщенных координат или обобщенные скорости нужно направлять в сторону увеличения обобщенных координат.