Билет 2

1) Вынужденные колебания в системе с одной степенью свободы. Исследование коэффициента динамичности.

Колебательное движение механической системы - такое движени, при котором все ее обобщенные координаты или хотя бы одна из них изменяется с неоднократным возрастанием и убыванием.

Вынужденные колебания в системе с одной степенью свободы.

Вынужденные колебания - колебания, возникающие под влиянием внешнего воздействия на тела и точки механической системы.

Дифференциальное уравнение вынужденных колебаний линейной системы с одной степенью свободы:

, где a>0; b0; c>0.

а - обобщенный коэффициент инерции; b - обобщенный коэффициент сопротивления; с - обобщенный коэффициент жесткости; Q(t) - обобщенная сила.

В случае, когда обобщенная сила Q(t), характеризующая внешнее воздействие на колебательную систему, изменяется во времени по закону синуса или косинуса:

,

где Q₀ - амплитуда обобщенной силы; p - частота обобщенной силы; - начальная фаза обобщенной силы, имеет место гармоническое возбуждение колебаний.

Амплитуда - наибольшее отклонение какой либо точки тела, совершающего колебания, от положения равновесия.

Частота - физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени, или проще: число периодов за одну секунду.

Фаза колебаний - физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени, или проще: аргумент синуса.

Гармонические колебания - колебания, при которых обобщенная координата изменяется во времени по закону синуса или косинуса.

Исследование коэффициента динамичности.

λ - коэффициент динамичности, т.е. отношение амплитуды установившихся вынужденных колебаний к статическому смещению.

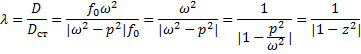
- коэффициент расстройки

D - амплитуда вынужденных колебаний.

f₀ = Q₀/a - амплитуда вынуждающего ускорения

p - частота вынужденных колебаний

- коэффициент затухания

- круговая или циклическая частота

Dст - статическое смещение системы от положения равновесия под действием постоянной силы, равной амплитудному значению гармонического возмущающего воздействия.

Q₀ - амплитуда обобщенной возмущающей силы Q(t)

2) Удар точки о неподвижную поверхность. Коэффициент восстановления.

Удар - механическое явление при котором происходит конечное измменение скоростей точки системы за очень малый промежуток времени.

Удар точки о неподвижную поверхность.

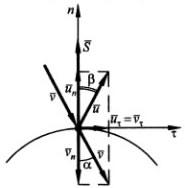
Материальная точка массы m падает на гладкую поверхность со скоростью , под углом (угол падения) к нормали (перпендикуляру) к поверхности (см. рисунок). После удара точка имеет скорость , направленную под углом (угол отражения) к нормали. Если , то удар точки о поверхность - косой, если =0 - прямой. Импульс ударной реакции поверхности направлен по нормали к поверхности.

Импульс силы (количество движения) - векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени.

Для определения скорости точки после удара и импульса ударной реакции воспользуемся теоремой об изменении количества движения точки, в проекциях на нормаль n и касательную .

Теорема об изменении количества движения (при ударе):

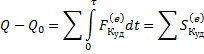
Следовательно: ; .

Отсюда: .

Для определения S и u_n необходимо знать коэффициент восстановления.

Коэффициент восстановления - отношение фазы восстановления к фазе деформирования, или отношение скорости после удара к скорости до удара.

Для определения коэффициента восстановления представим удар точки о поверхность в двух фазах. В начале фазы деформирования скорость точки равна , в конце - . Импульс ударной реакции в этой фазе:

,

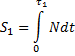где 1- время фазы деформирования; N - нормальная ударная реакции поверхности.

В конце фазы деформирования нормальная составляющая скорости точки равна нулю и (где - качательная составляющая скорости точки).

Фаза восстановления начинается при скорости точки и заканчивается, когда точка покидает поверхность со скоростью . Импульс ударной реакции в этой фазе:

.

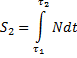Согласно теореме об изменении количества движения точки в проекции на нормаль для первой и второй фаз удара соответственно имеем:

; .

Заметим, что S₁ + S₂ = S. Разделив уравнение S₂ на S_1, получим уравнение для коэффициента восстановления:

.

Коэффициент восстановления определяют экспериментально. Если K=1 удар называют абсолютно упругим и при K=0 - абсолютно неупругим, а при 0<K<1 - упругим. Если K=0 - фаза восстановления отсутствует.

При прямом ударе (=0) коэффициент восстановления можно определить экспериментально:

,

где h₁ - высота падения; h₂ - высота отскока.

При косом ударе :

.

При известном коэффициенте восстановления K можно решить задачу об определении и с помощью дополнительной зависимости:

, так как .