5) Понятие о криволинейных координатах. Координатные линии и координатные оси.

Движение точки в пространстве можно считать заданным, если известны законы изменнеия трех ее декартовых координат x, y, z как функции времени. Однако в некоторых случаях пространственного движения материальных точек (например, в областях, ограниченных поверхностями различной формы) использование уравнений движения в декартовых координатах неудобно, так как они становятся слишком громоздкими. В таких случаях можно выбрать другие три независимых скалярных параметра q1, q2, q3, называемых криволинейными, или обобщенными координатами, которые также однозначно определяют положение точки в пространстве.

Тогда радиус-вектор точки может быть выражен функцией как декартовых, так и криволинейных координат: . При этом следует иметь в виду, что декартовы координаты точки могут также быть выражены в виде функций, зависящих от криволинейных координат: . Для задания движения точки в криволинейных координатах необходимо иметь уравнения движения точки в виде: .

Характеристиками криволинейной системы координат являются координатные линии и координатные оси.

Координатные линии (qi), проходящие через любую выделенную точку М пространства с фиксированными значениями координат q1M, q2M, q3M и соответствующие каждой i-ой криволинейной координате, можно определить как годограф радиус-вектора riM точки М, изменяющегося в результате варьирования одной выделенной i-ой криволинейной координаты при условии, что другие сохраняются постоянными и равными их значениям в выделенной точке:

Касательная к i-ой координатной линии в данной точке называется координатной осью Mqi, относящейся к i-ой криволинейной координате в данной точке. Положительные направления координатных осей задаются единичными векторами, которые называются базисами. Они определяются через частные производные от радиус-вектора точки по i-ой обобщенной координате в данной точке M: 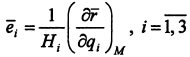. Здесь 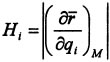- параметр, который называется i-ым коэффициентом Ламе и равен значению модуля частной производной от радиус-вектора точки по i-ой криволинейной координате, вычисленной в данной точке М. Каждый из векторов ei имеет направление, соответствующее направлению движения точки конца радиус-вектора riM при возрастанийй i-ой обобщенной координаты.