8) Вращение твердого тела вокруг неподвижной оси. Скорости и ускорения точек тела (векторные и скалярные выражения).

Вращением твердого тела вокруг неподвижной оси (или просто вращательным движением) называется такое движение твердого тела, при котором в теле можно выделить прямую, все точки которой будут оставаться неподвижными во время движения. Эта прямая называется осью вращения твердого тела. Очевидно, что для ее задания достаточно указать как минимум две неподвижные точки в рассматриваемом теле, через которые она проходит.

Алгоритм задания вращательного движения может быть определен на основе следующего анализа. Введем неподвижную прямоугольную декартову систему координат Oxyz и аналогичную подвижную систему координат OXYZ, жестко связанную с рассматриваемым телом, расположив оси Oz и OZ на оси вращения тела (рис.).

Пусть в начальный момент времени оси координат подвижной и неподвижной систем совпадали. Тогда положение вращающегося тела относительно неподвижной системы координат в любой текущий момент времени однозначно определится значением двугранного угла "фи" между неподвижной плоскостью Oxz и подвижной плоскостью OXZ, вращающейся вместе с рассматриваемым телом. Таким образом, при вращении вокруг неподвижной оси тело имеет одну степень свободы, так как его положение в неподвижной системе координат Oxyz однозначно определяется значением одного скалярного параметра — угла "фи". Уравнение, определяющее изменение этого угла как функции времени, общего вида: "фи" = "фи"(t), где "фи"(t) — непрерывная дважды дифференцируемая функция времени, называется законом вращения твердого тела вокруг неподвижной оси.

Угловую скорость можно определить и как вектор "омега", расположенный на оси вращения и равный , где k — единичный вектор, задающий положительное направление оси вращения, или орт оси Oz (рис.).

Проекция вектора угловой скорости на ось вращения Oz: , т.е. она равна угловой скорости вращения тела. Положительные направления отсчета и оси Oz соответствуют правой декартовой системе координат.

Численное значение угловой скорости "омега" равно модулю вектора "омега" и определяется как модуль проекции "омега"z либо как модуль угловой скорости тела при его вращении вокруг неподвижной оси: .

Единица измерения угловой скорости в СИ — радиан в секунду (рад/с).

Изменение угловой скорости тела во времени характеризуется его угловым ускорением.
Угловым ускорением тела называется первая производная от угловой скорости или вторая производная по времени от угла поворота вокруг неподвижной оси: 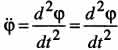, где - скаляоная алгебраическая величина.

Как векторную величину угловое ускорение можно определить так: .

Проекция углового ускорения на ось вращения Oz: , т.е. она равна угловому ускорению тела. Положительные направления отсчета , и оси Oz соответствуют правой декартовой системе координат.

Значение (модуль) углового ускорения: .

Единица измерения углового ускорения в СИ - радиан на секунду в квадрате (рад/с2).