Билет 5

1) Свободные колебания системы с одной степенью свободы. Фаза, период, частота и амплитуда колебаний.

Колебательное движение механической системы - такое движени, при котором все ее обобщенные координаты или хотя бы одна из них изменяется с неоднократным возрастанием и убыванием.

Свободные колебания системы с одной степенью свободы.

Свободные колебания (собственные колебания) - колебания в любой колебательной системе, происходящие в отсутствие внешнего воздействия.

Дифференциальное уравнение свободных колебаний системы с одной степенью свободы:

, где a>0; b0; c>0.

а - обобщенный коэффициент инерции; b - обобщенный коэффициент сопротивления; с - обобщенный коэффициент жесткости.

В случае если система консервативная, т.е. b=0, дифференциальное уравнение движения принимает форму:

, где - круговая или циклическая частота.

Запишем дифференциальное уравнение в виде:

.

C₁ и C₂ - произвольные постоянные, которые мы определим из начальных условий: при t=0 q=q₀, .

Отсюда C₁=q₀; .

Введем новые произвольные постоянные:

;

и представим решение дифференциального уравнения в амплитудной форме:

.

Амплитуда (А) - наибольшее отклонение какой либо точки тела, совершающего колебания, от положения равновесия.

Произвольные постоянные А и выражаются через начальные условия следующим образом:

; .

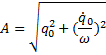Зависимость q(t) представлена на рисунке.

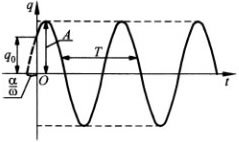
Гармонические колебания - колебания, при которых обобщенная координата изменяется во времени по закону синуса или косинуса.

Свободные колебания с одной степенью свободы являются гармоническими.

Характеристики гармонических колебаний:

- круговая, или циклическая частота, измеряемая в секундах в минус первой степени;

- фаза колебаний;

Фаза колебаний - физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени, или проще: аргумент синуса.

- начальная фаза колебаний;

А - амплитуда колебаний;

Т - период колебаний - время в секундах. за которое фаза колебаний изменится на

.

В инженерной практике используют величину, обратную периоду колебаний, называемую частотой колебаний

и измеряемую в герцах (Гц).

Круговая частота , период колебаний Т и частота не зависят от начальных условий, поэтому их называют собственными характеристиками колебательной системы.

Свойство независимости частоты и периода колебаний от начальных условий - свойство изохронности колебаний - связано с линейностью дифференциального уравнения и, следовательно, с допущением о малости колебаний.

2) Общие теоремы динамики в случае удара. Изменение угловой скорости при ударе по вращающемуся твердому телу.

Теорема об изменении количества движения.

В проекциях на оси:

Для точки в системе:

+ ...

Законы сохранения количества движения:

1) Если сумма , то и , т.е. если векторная сумма внешних ударных импульсов действующих на систему равно нулю, то векторы и остаются постоянными, при этом внутри системы могут быть ударные импульсы;

2) Если , то и .

Теорема об изменении кинетического момента.

Теорема об изменении кинетической энергии.

(про теоремы из лекций можно посмотреть в вопросе 36. Теоремы об изменении количества движения, кинетического момента и кинетической энергии точки и механической системы при ударе.)