Билет 16

1) Затухающее неколебательное движение в случае "критического" сопротивления.

Колебательное движение механической системы - такое движени, при котором все ее обобщенные координаты или хотя бы одна из них изменяется с неоднократным возрастанием и убыванием.

Устойчивое равновесие - равновесие, при котором малое возмущение системы приводит к ее малому отклонению от состояния равновесия.

Равновесие тела устойчиво:
- если его потенциальная энергия имеет минимальное значение;
- если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями.

Дифференциальное уравнение малых движений системы с линейным сопротивлением имеет вид:

,

где - коэффициент затухания; - круговая или циклическая частота.

а - обобщенный коэффициент инерции; b - обобщенный коэффициент сопротивления; с - обобщенный коэффициент жесткости.

Характерестическое уравнение:

.

Корни характерестического уравнения:

.

Характер движения системы будет существенно зависеть от соотношения между величинами и . Возможны три случая:

1) < - случай малого сопротивления, уравнение имеет комплексно-сопряженные корни;

2) = - случай критического сопротивления (резонанс), уравнение имеет кратные корни;

3) > - случай большого сопротивления, уравнение имеет два вещественных отрицательных корня.

Затухающее неколебательное движение мы имеем в случае критического сопротивления (=) и в случае большого сопротивления (>).

Рассмотрим случай =.

При кратных корнях общее решение дифференциального уравнения имеет вид:

.

При начальных условиях t=0 q=q₀, :

C₁=q₀; .

Решение ДУ может обратиться в ноль только один раз, если константы C₁ и C₁ разные знаки. Для этого начальное отклонение и начальная скорость должны иметь разные знаки, и при этом необходимо выполнение условия .

Видно, что движение не имеет колебательного характера и отсутствуют какие-либо признаки периодичности. Такое движение называют апериодическим, а с учетом рассмотрения критического сопротивления - предельно апериодическим.

2) Основные положения и допущения теории удара.

Удар - механическое явление при котором происходит конечное измменение скоростей точки системы за очень малый промежуток времени.

При , .

Основные положения теории удара:

1) Все теоремы динамики записываются в интегральной форме;

Теорема об изменении количества движения:

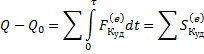
Теорема об изменении кинетического момента:

Теорема об изменении кинетической энергии:

Применяются полные импульсы ударных сил.

2) Перемещением материальных точек пренебрегают;

3) Неучитывают действие неударных сил;

4) Пренебрегают ударным трением, так как оно не подчиняется законам Кулона;

5) Вводят понятие коэффициент восстановления:

Коэффициент восстановления - отношение фазы восстановления к фазе деформирования, или отношение скорости после удара к скорости до удара.

Для определения коэффициента восстановления представим удар точки о поверхность в двух фазах. В начале фазы деформирования скорость точки равна , в конце - . Импульс ударной реакции в этой фазе:

,

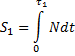где 1- время фазы деформирования; N - нормальная ударная реакции поверхности.

В конце фазы деформирования нормальная составляющая скорости точки равна нулю и (где - качательная составляющая скорости точки).

Фаза восстановления начинается при скорости точки и заканчивается, когда точка покидает поверхность со скоростью . Импульс ударной реакции в этой фазе:

.

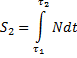Согласно теореме об изменении количества движения точки в проекции на нормаль для первой и второй фаз удара соответственно имеем:

; .

Заметим, что S₁ + S₂ = S. Разделив уравнение S₂ на S_1, получим уравнение для коэффициента восстановления:

.

Коэффициент восстановления определяют экспериментально. Если K=1 удар называют абсолютно упругим и при K=0 - абсолютно неупругим, а при 0<K<1 - упругим. Если K=0 - фаза восстановления отсутствует.

При прямом ударе (=0) коэффициент восстановления можно определить экспериментально:

,

где h₁ - высота падения; h₂ - высота отскока.

При косом ударе :

.

При известном коэффициенте восстановления K можно решить задачу об определении и с помощью дополнительной зависимости:

, так как .

(дополнительно можно посмотреть 35. Основные положения теории удара.)