Билет 17

1) Потенциальное силовое поле. Элементарная и полная работа силы в потенциальном силовом поле.

Силовым полем называют часть пространства в каждой точке которого на материальную точку действует сила зависящая от координат.

Если сила не зависит от времени, то силовое поле называется стационарным, если не зависит - нестационарным.

Силовое поле - потенциальное, если имеется силовая функция U, зависящая от координат.

Например, в декартовой системе координат: U(x,y,z,t)

- потенциальное силовое поле

Вектор-градиент скалярной величины:

Основные свойства U стационарного потенциального силового поля.

Полная работа силы не зависит от пути перемещения.

Полная работа силы поля на каком-либо перемещении равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории (если силовая функция является однозначной) (при нестационарном поле это определение полной работы не действует).

Частный случай: Работа силы потенциального силового поля равна нулю, при перемещении точки по замкнутой траектории.

Силовые линии потенциального силового поля (ПСП) - линии, в каждой точке которых сила направлена по касательной к этой линии.

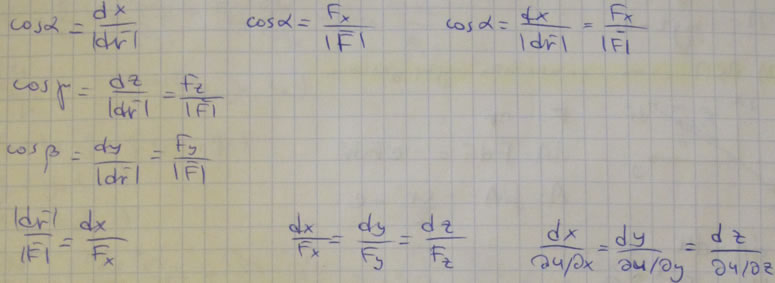
Потенциальной энергией (П) потенциального силового поля (ПСП) в заданной точке называется работа, которую совершают силы поля при перемещении материальной точки из данной точки в начальную.

П = A_MMo = U₀ - U = C₀ - U = -U

A_MMo = U₀ - U

Для всех точек U₀=const одинаковое.

П = -U + const

Потенциальную энргию какой либо точки ПСП с точностью до константы можно определить как значение U в этой точке со знаком "минус" (-U).

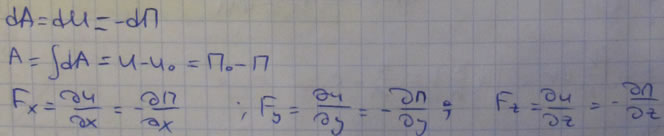
Поверхности уровня - поверхности, все точки которых имеют одинаковые значения силовой функции.

U(x,y,z)=C

Свойства поверхностей уровня:

1) Работа силы равна нулю, если начальные и конечные точки перемещения лежат на одном уровне.

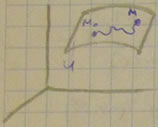
A=U - U₀=U - U=0

2) Сила потенциального силового поля (ПСП) всегда перпендикулярна плоскости касательной к поверхности уровня.

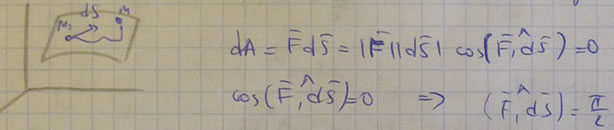
3) Сила всегда направлена в сторону возрастания силовой функции.

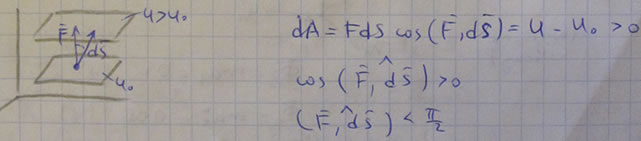
4) Если поверхности уровня сближаются, то сила возрастает.

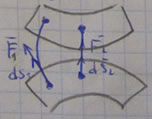
A=F₁S₁=F₂S₂

(подробнее 08. Потенциальное силовое поле. Силовая функция и потенциальная энергия поля. Поверхности уровня и их свойства.)

2) Основные положения теории удара. Теорема об изменении кинетического момента при ударе.

Удар - механическое явление при котором происходит конечное измменение скоростей точки системы за очень малый промежуток времени.

При , .

Основные положения теории удара:

1) Все теоремы динамики записываются в интегральной форме;

Теорема об изменении количества движения:

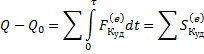
Теорема об изменении кинетического момента.

Теорема об изменении кинетической энергии:

Применяются полные импульсы ударных сил.

2) Перемещением материальных точек пренебрегают;

3) Неучитывают действие неударных сил;

4) Пренебрегают ударным трением, так как оно не подчиняется законам Кулона;

5) Вводят понятие коэффициент восстановления:

Коэффициент восстановления - отношение фазы восстановления к фазе деформирования, или отношение скорости после удара к скорости до удара.

Для определения коэффициента восстановления представим удар точки о поверхность в двух фазах. В начале фазы деформирования скорость точки равна , в конце - . Импульс ударной реакции в этой фазе:

,

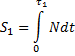где 1- время фазы деформирования; N - нормальная ударная реакции поверхности.

В конце фазы деформирования нормальная составляющая скорости точки равна нулю и (где - качательная составляющая скорости точки).

Фаза восстановления начинается при скорости точки и заканчивается, когда точка покидает поверхность со скоростью . Импульс ударной реакции в этой фазе:

.

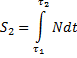Согласно теореме об изменении количества движения точки в проекции на нормаль для первой и второй фаз удара соответственно имеем:

; .

Заметим, что S₁ + S₂ = S. Разделив уравнение S₂ на S_1, получим уравнение для коэффициента восстановления:

.

Коэффициент восстановления определяют экспериментально. Если K=1 удар называют абсолютно упругим и при K=0 - абсолютно неупругим, а при 0<K<1 - упругим. Если K=0 - фаза восстановления отсутствует.

При прямом ударе (=0) коэффициент восстановления можно определить экспериментально:

,

где h₁ - высота падения; h₂ - высота отскока.

При косом ударе :

.

При известном коэффициенте восстановления K можно решить задачу об определении и с помощью дополнительной зависимости:

, так как .

(дополнительно можно посмотреть 35. Основные положения теории удара.)