Билет 23

1) Силовая функция и потенциальная энергия потенциального силового поля. Условия существования силовой функции. Закон сохранения механической энергии.

Закон сохранения механической энергии.

Сумма кинетической и потенциальной энергии называется полной энергией Е механической системы. Системы, для которых выполняется закон, сохранения механической энергии, называются консервативными.

Формула (15.114) выражает закон сохранения механической энергии для механической системы: если все силы, действующие на систему, потенциальны, то при движении системы ее полная механическая энергия постоянна.

Следует отметить, что закон сохранения механической энергии справедлив и в том случае, когда кроме потенциальных имеются и непотенциальные силы, но которые при движении системы не совершают работы.

(дополнительно можно посмотреть 08. Потенциальное силовое поле. Силовая функция и потенциальная энергия поля. Поверхности уровня и их свойства.)

2) Основные положения теории удара. Теорема об изменении количества движения при ударе.

Удар - механическое явление при котором происходит конечное измменение скоростей точки системы за очень малый промежуток времени.

При , .

Основные положения теории удара:

1) Все теоремы динамики записываются в интегральной форме;

Теорема об изменении количества движения:

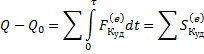
Теорема об изменении кинетического момента:

Теорема об изменении кинетической энергии:

Применяются полные импульсы ударных сил.

2) Перемещением материальных точек пренебрегают;

3) Неучитывают действие неударных сил;

4) Пренебрегают ударным трением, так как оно не подчиняется законам Кулона;

5) Вводят понятие коэффициент восстановления:

Коэффициент восстановления - отношение фазы восстановления к фазе деформирования, или отношение скорости после удара к скорости до удара.

Для определения коэффициента восстановления представим удар точки о поверхность в двух фазах. В начале фазы деформирования скорость точки равна , в конце - . Импульс ударной реакции в этой фазе:

,

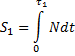где 1- время фазы деформирования; N - нормальная ударная реакции поверхности.

В конце фазы деформирования нормальная составляющая скорости точки равна нулю и (где - качательная составляющая скорости точки).

Фаза восстановления начинается при скорости точки и заканчивается, когда точка покидает поверхность со скоростью . Импульс ударной реакции в этой фазе:

.

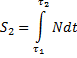Согласно теореме об изменении количества движения точки в проекции на нормаль для первой и второй фаз удара соответственно имеем:

; .

Заметим, что S₁ + S₂ = S. Разделив уравнение S₂ на S_1, получим уравнение для коэффициента восстановления:

.

Коэффициент восстановления определяют экспериментально. Если K=1 удар называют абсолютно упругим и при K=0 - абсолютно неупругим, а при 0<K<1 - упругим. Если K=0 - фаза восстановления отсутствует.

При прямом ударе (=0) коэффициент восстановления можно определить экспериментально:

,

где h₁ - высота падения; h₂ - высота отскока.

При косом ударе :

.

При известном коэффициенте восстановления K можно решить задачу об определении и с помощью дополнительной зависимости:

, так как .

(дополнительно можно посмотреть 35. Основные положения теории удара.)